Fact. Assume $\mathbb{R}\neq \mathbb{R}^L$, then any uncountable $\Pi^1_1$ set has a perfect subset if and only if it is not a subset of $L$.

This is exercise-left-to-reader from

  • Mansfield, Richard. “Perfect subsets of definable sets of real numbers.” Pacific Journal of Mathematics 35, no. 2 (1970): 451-457.

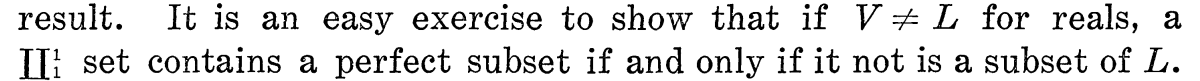
image1

Proof. The Mansfield-Solovay Theorem states that if a $\Sigma^1_2$ set has an unconstructible element, then it has a perfect subset coming from a perfect tree coded in $L$ (and this relativizes). So this takes care of the right-to-left direction. On the other hand, if $X$ is $\Pi^1_1$ and has a perfect subset, then by Shoenfield absoluteness there is a perfect tree in $L$ whose branches are (a subset) of the set defined by the same $\Pi^1_1$ formula. Using any $r\in 2^\omega \smallsetminus L$ as a guide for going left or right going down that tree, we can obtain a real that cannot be in $L$. This is because if it were in $L$, then we’d be able to recover $r$ and that’s a contradiction.