Being reals of a model of set theory a special property
(Another #lolbvious post, because it’s one of those things that’s supposed to be obvious/clear/straightforward/true by the usual argument… etc, but just makes you go lol, yeah right)
The following screenshot is taken from the notes of Jörg Brendle’s Bogotá lectures on forcing and the structure of the real line.
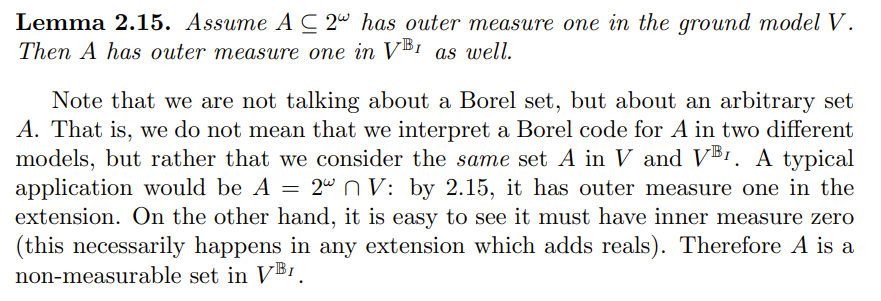
This post provides a proof or two of the remark that in any extension which adds reals, the ground model reals have inner measure zero.
Theorem. Assume \(M\) is a model of ZFC, possibly a proper class. If there is a real number not in \(M\), then the reals in \(M\) have inner measure zero.
Proof using \([0,1]\). Letting \(a\) denote a real not in \(M\), consider the translates \(A_n=\{r+\frac{a}{n}\mid r\in [0,1^M]\}\). The \(A_n\)’s are pairwise disjoint, because otherwise (say \(q+\frac{a}{n}=r+\frac{a}{m}\)) \(a\) would have been definable in \(M\) as the unique real solution to the equation \(q+\frac{x}{n}=r+\frac{x}{m}\), contradicting the assumption that \(a\notin M\).
But translation preserves inner measure, and \(\bigcup_n A_n\) is bounded. So if \([0,1]^M\) has inner measure anything other than zero, then \(\bigcup_n A_n\) would have inner measure infinity, contradicting boundeness. \(\square\)
Proof using \(2^\omega\). Given a real \(a\notin M\), consider the flip maps induced by \(a\). That is, for each natural number \(n\), let \(F_n\) flip the \((n+k)^\text{th}\) bit of \(x\in 2^\omega\) iff \(a(k)=1\). In other words, \(F_n(x)(n+k)=1-x(n+k)\) iff $a(k)=1$, otherwise \(F_n(x)(n+k)=x(n+k)\). Now mirroring the proof above, let \(A_n=F_n[(2^\omega)^M]\).
First notice that if \(F_n(x)=F_m(y)\) for \(n\neq m\), then \(x\neq y\) (This is most easily proven by looking at the contrapositive and using the fact that \(a\) has at least one \(1\)). Next, I claim that the \(A_n\)’s must be disjoint. This is because if \(F_n(x)=F_m(y)\) for \(n\neq m\), then \(a\) is definable as the unique real that makes this true (recall that the \(F\)’s are defined from \(a\)).
To see why \(a\) is unique: suppose not, then there are \(a\neq a'\) witnessing the corresponding \(F_n(x)=F_m(y)\) and \(F'_n(x)=F'_m(y)\). Now let \(k\) be the first place that \(a\) differs from \(a'\) and assume without loss of generality that \(a(k)=0\) and \(n<m\).
Observe: \(F_m(y)(n+k)=F'_m(y)(n+k)\). This is because if \(n+k<m\), then the equality holds by definition of \(F_m\) and \(F'_m\). On the other hand, if \(n+k=m+l\) for some \(l\), then \(a(l)=a'(l)\) by minimality of \(k\) and the assumption that \(n<m\). Hence \(F_m(y)(m+l)=F'_m(y)(m+l)\).
Now to arrive at a contradiction, notice that we have:
\[\begin{align*} F_n(x)(n+k) & = F_m(y)(n+k)\\ & = F'_m(y)(n+k) \\ & = F'_n(x)(n+k) \end{align*}\]But this cannot be true, since \(a\) tells \(F_n\) to keep the \((n+k)^\text{th}\) bit of \(x\), whereas \(a'\) tells \(F'_n\) to flip it. \(\square\)
The lemma before the remark is meant to show that random forcing preserves outer measure. So after forcing to add a random real, the ground model reals have outer measure 1 but inner measure 0, making it non-measurable. Similarly, after adding a Cohen real, the ground model reals don’t have the property of Baire.